A probabilidade da bolsa subir esse ano acabou de aumentar
Pelo menos é isso que diz o Teorema de Bayes.
No mês de janeiro a bolsa brasileira subiu 4,86%. Essa informação muda a probabilidade do IBOV fechar 2025 positivo? Para responder essa pergunta precisamos entender o conceito de probabilidade condicional.
A ideia de que a chance de um resultado acontecer muda dadas as circunstâncias é intuitiva para todos nós. Por exemplo: qual a probabilidade do Vasco vencer no fim de semana? (Não me venha dizer "baixa"). Agora, qual a probabilidade do Vasco ganhar a partida dado que o time adversário é o Real Madrid?
Relembremos que probabilidade, de forma simplificada, é a quantidade de vezes que um determinado evento ocorre dentro de um espaço amostral. Por exemplo, podemos dizer que se um time ganhou X vezes nas últimas Y partidas, então a probabilidade de vitória é X/Y.
No entanto, quando adicionamos a condição de que o time adversário é um específico, isso muda o nosso espaço amostral. Agora não são mais Y partidas, mas um subconjunto delas. Portanto, a probabilidade muda.
Na vida real estamos sempre recebendo informações novas, e um modelo matemático pode se atualizar para refletir as novas probabilidades dadas as novas informações. Portanto, repito a pergunta: sabendo que o IBOV subiu 4,86% em janeiro, quais são as chances dele fechar 2025 positivo?
Esse assunto foi o tema do meu último vídeo no YouTube, onde utilizei o novo modelo de reasoning do ChatGPT, o o3-mini-high, para calcular a probabilidade usando apenas matemática, e não código. Confira!
Antes de dizer sobre como responder essa questão de forma matemática, vamos logo à resposta. Nos últimos 25 anos, a bolsa fechou positiva 15 vezes. Olhando para esse espaço amostral podemos dizer que a probabilidade de alta num ano qualquer é de 15/25 ou 60%.
Mas não estamos num ano qualquer: houve um evento que atualizou o modelo, o fato do primeiro mês do ano ter sido positivo. Olhando para esse recorte, temos 10 anos onde janeiro subiu. E em 9 dessas 10 ocorrências o ano em questão fechou positivo. Sendo assim, podemos concluir que a condição "janeiro > 0" joga a probabilidade de alta para 90%!
É claro que pelo espaço amostral reduzido é fácil simplesmente contar as ocorrências e calcular a probabilidade. Mas esse conceito é explicado pelo Teorema de Bayes:
Ora, se considerarmos A como os eventos onde o IBOV termina o ano positivo, e B como os eventos onde janeiro fecha positivo, lemos P(A | B) como a probabilidade do IBOV fechar positivo (A) dado que janeiro fechou positivo (B).
O Teorema de Bayes nos permite entender como um evento influencia a probabilidade de outro, assim como nossa probabilidade de fazer uma trinca num jogo de poker aumenta se seguramos um par nas mãos.
O cálculo tanto P(A) quanto P(B) é direto: contamos a ocorrência de cada evento no espaço amostral de 25 anos, o que nos dá P(A) = 15/25 (probabilidade de que o ano seja positivo) e P(B) = 10/25 (probabilidade de que janeiro seja positivo).
Resta-nos definir P(B | A), ou a probabilidade de que janeiro seja positivo dado que o ano foi positivo. Ora, já vimos que o IBOV subiu em 15 das últimas 25 vezes, portanto nosso espaço amostral agora é 15. Em 9 dessas vezes janeiro foi positivo, de modo que P(B | A) = 9/15.
Substituindo os valores no teorema de Bayes chegamos a:
Os mesmos 90% que havíamos chegado inicialmente.
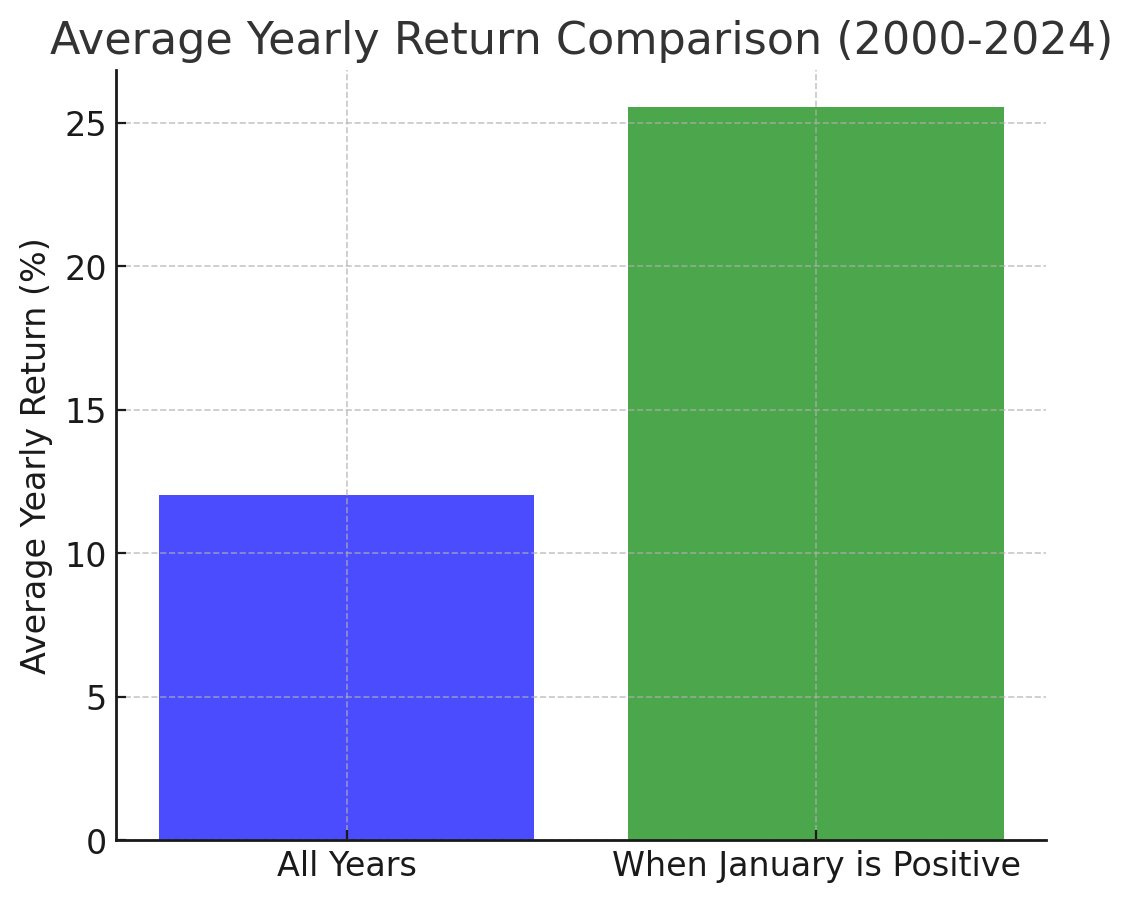
Talvez mais interessante do que a probabilidade de retorno é calcular o retorno anual médio. Ou seja, o fato de haver uma alta em janeiro pode ser considerado um preditor de que o retorno anual aumentará?
Foi justamente isso que calculei nesse gráfico acima. O retorno anual médio do IBOV desde 2000, independente de qualquer condição, é de 12,02%. Quando adicionamos a condição de que janeiro foi positivo, esse retorno dobra para 25,55%!
É claro que essa generalização é apenas um exercício. O espaço amostral é consideravelmente pequeno para considerarmos essa estatística como um número sólido. Meu intuito aqui é explicar o conceito de probabilidade condicional e o fato de que à medida que aprendemos novas informações, um modelo quantitativo pode ser capaz de incorporá-las e atualizar sua predição.
No mais, resta-nos especular se existe alguma causalidade: numa bolsa influenciada por players externos como a nossa, seria o primeiro mês do ano fechar no azul um preditor de que haverá um fluxo positivo para todo o ano? Vai saber. Melhor nos restringirmos apenas à matemática.